毕达哥拉斯与勾股定理 毕达哥拉斯树
http://www.newdu.com 2024/11/24 10:11:43 未知 佚名 参加讨论
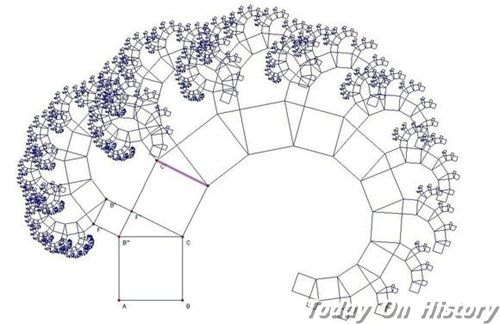 毕达哥拉斯树 毕达哥拉斯在数学上最为人所知的贡献恐怕要属勾股定理的提出与证明。这一定理在生活中的应用非常的广泛,而毕达哥拉斯也根据这一定理画出了结构精巧、极富美感的毕达哥拉斯树。 毕达哥拉斯与勾股定理 勾股定理是一个基本的几何定理,它的内容是直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a?+b?=c? 。 远在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。古埃及人在建筑宏伟的金字塔和尼罗河泛滥后测量土地时,也应用过勾股定理。在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。而在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。 毕达哥拉斯树 毕达哥拉斯树是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形。又因为重复数次后的形 状好似一棵树,所以被称为毕达哥拉斯树,也叫“勾股树”。 在毕达哥拉斯树中,两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。而同一次数的所有小正方 形面积之和等于最大正方形的面积,直角三角形两个直角边平方的和等于斜边的平方。 利用不等式A^2+B^2≥2AB可以得出以下结论:三个正方形之间的三角形,其面积小于等于大正方形面积的四分 之一,大于等于一个小正方形面积的二分之一。根据所做的三角形的形状不同,重复做这种三角形的毕达哥拉 斯树的“枝干”茂密程度就不同。毕达哥拉斯在数学上最为人所知的贡献恐怕要属勾股定理的提出与证明。这一定理在生活中的应用非常的广泛,而毕达哥拉斯根据这一定理画出了结构精巧、极富美感的毕达哥拉斯树。 毕达哥拉斯与勾股定理 勾股定理是一个基本的几何定理,它的内容是直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,设直角三角形两直角边为a和b,斜边为c,那么a?+b?=c? 。 远在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。古埃及人在建筑宏伟的金字塔和尼罗河泛滥后测量土地时,也应用过勾股定理。在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。而在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。 毕达哥拉斯树 毕达哥拉斯树是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形。又因为重复数次后的形 状好似一棵树,所以被称为毕达哥拉斯树,也叫“勾股树”。 在毕达哥拉斯树中,两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。而同一次数的所有小正方 形面积之和等于最大正方形的面积,直角三角形两个直角边平方的和等于斜边的平方。 利用不等式A^2+B^2≥2AB可以得出以下结论:三个正方形之间的三角形,其面积小于等于大正方形面积的四分 之一,大于等于一个小正方形面积的二分之一。根据所做的三角形的形状不同,重复做这种三角形的毕达哥拉 斯树的“枝干”茂密程度就不同。 (责任编辑:admin) |