|
二、《续古摘奇算法》中的正斛法及其捷法运算 “斛”是我国古代容量单位,它的变动关乎民生大计,故杨辉在《续古摘奇算法》中用专篇来讨论“正斛法”,足见其对这个问题的重视程度。杨辉对“斛”制变革的历史做了这样的描述: 《夏侯阳》仓曹云:古者凿池,方一尺,深一尺六寸二分,受粟一斛。至汉王莽改铸铜斛,用深一尺九寸二分。至宋元嘉二年,徐受重铸,用二尺三寸九分。至梁大同元年,甄鸾校之,用二尺九寸二分。然异时事变,斗尺(斛)不同,以古就今,临时较定,始可行用。若欲审之,以掘地作穴,方广三尺已下。以今时斗,量米一斛,置诸穴中,概令平满,如有少剩,临时增减,取米适平,然后出之,径量以知深浅,乃可为斛法定数。辉伏睹京城见用官斗号杭州百合,浙郡一体行用。未较积尺积寸者,盖斗势上阔下狭,维板凸突,又有提梁,难于取用。况栲栳藤斗,循习为之。今将官升与市尺较订,少补日用之万一。每立方三寸,谓四维各三寸,高三寸,积二十七寸。受粟一升;每方五寸,深五寸四分,积一百三十五寸。受粟五升;每方一尺,深二寸七分,积二百七十寸。受粟一斗;每方一尺,深一尺三寸五分,受粟五斗。(28) 关于此段量制史料,吴文俊主编《中国数学史大系》第5卷及郭正忠《三至十四世纪中国的权衡度量》等都有较细致的阐释。其中尤为值得注意的现象是宋代的斛制非常混乱,既有中央朝廷之量、各种地方官量、专用官量以及军量和学量等,同时又有乡村居民以及城镇工商业自制和使用的民间量器,加上因“栲栳藤”本身的原因,制作很不规则,“既有按法量或官量规格复制的合法量器,也有违反规格私造而应予取缔的非法量器,还有本属非法而又为官府所默许、认可的量器”等。(29)为了增收多取,官府往往加大量器来收取,是谓“加耗”,名色至多。此外,尚有20多种加斛与加斗,从而使民众的税负更加沉重。所以,宋代斛制的变化反映了统治阶级残酷剥削的一面,而从数学史的角度,我们通过对量斛的容积换算,无疑能够加深对其剥削性质的认识。宋代浙尺有3种形制:27.4厘米、28.3厘米及31厘米。依此计算,则宋代的“杭州百合”官斗分别为: 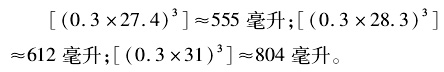 宋代以前,以十斗为一斛,而北宋末南宋初则改五斗为一升。(30)斛型无定制:“既有圆体五斗斛,又有方体五斗斛;既有敞口斛,又有狭口斛。”(31)正是在这样的历史背景下,杨辉才提出了“正斛法”的主张,即提出订正容量单位的标准。 在“正斛法”下,有“求圆斛术”,主要讲述立方体量器与圆柱体量器等容积的换算方法。然而,杨辉给出的却是其“方体五斗斛”的基本标准:“每方一尺,深二尺七寸,受粟一石。”(32)此类官斛的容积为2700立方寸,若仍按上述宋代厘米尺计算,则1石斛容量分别为:55541毫升、61196毫升和80436毫升,是前述官升容积的100倍。 于是,如何简化不同斛石之间的计量与折算,就成为杨辉《乘除通变算宝》卷中的主要内容之一。下面是杨辉给出的一道例题:“(米)足斛二百二十九石八升,问为八斗三升法斛几何?答曰:二百七十六石。”(33)又《法算取用本末》卷下载:“米八百九十石,每石省斛八斗三升,问为足斛几何?答曰:七百三十八石七斗。”(34)题中出现了足斛与省斛之间的换算。据郭正忠研究,宋代仅斛型至少有13种以上,其量制有135升之石,110升之石,83升之石,65升之石等多种,此处“省斛(83升)之一石,即为省斛(83升)之一斛,仅为足斛容积的0.83石”。(35) 此外,还有足秤与省秤之间的折算,如题云:“足秤一百二十六斤,问为省秤多少?答曰:一百五十七斤半。”(36)“足秤二百三十二斤,问展省秤多少?答曰:二百九十斤。”(37)在这里,“足秤”是指200钱或20两为1斤的秤,而“省秤”则是指16两为1斤之“官司省秤”,两者的比例为20∶16,或10∶8,或5∶4。(38)故方回在《续古今考》中述及:“有定秤二百文铜钱重,有二百二十钱秤。民间买卖行用,鱼肉二百钱秤,薪炭粗物二百二十钱秤。官司省秤十六两,计一百六十钱重。民间金、银、珠宝、香药细色,并用省秤。”(39) 可见,200铜钱重即20两,此为“足秤”或云“足斤”,行用于“民间买卖”及“鱼肉”买卖。220铜钱重即22两,此为“加秤”或云“加斤”,行用于民间“薪炭粗物”买卖。160铜钱重即16两,此为“省秤”或云“省斤”,行用于官府及“民间金、银、珠宝、香药细色”等买卖。当然,南宋官民因不同地区和不同专业部门,所行用的秤衡及斤两制度亦各不相同,实际情形比较复杂。仅江浙地区就有4种秤,“收谷一秤,十六斤,二百足铜钱为一斤。或十五斤,十四斤。糯谷,十三斤。所至江浙不同”。(40)所以在这里,杨辉固然旨在普及算法知识,但从客观上看,其却积极推动了政府统一秤衡与斤两制度。《日用算法》有题云:“今有物一百一十二斤,足秤,问为省秤几何?答曰:一百四十斤。”(41) 根据题中术文“以斤数为实,身外加二五”(42)知,杨辉在题中所用是标准的“足秤”与“省秤”,则依题意,有112斤×20/16=112斤×1.25=140斤。 又题云:“今有物三百九十一斤四两,省秤。问足秤几何?答曰:三百一十三斤。”(43) 由上题算法知,(391+4/16斤)×16/20=391.25斤×0.8=313斤。 在宋代,度量衡制改为十进位后,斤两仍为十六进位制,计算时比较繁复和麻烦。因此,杨辉在《日用算法》中编制了“斤价化两价”歌诀,以简化计算。其诀云:“一求,隔位六二五;二求,退位一二五;三求,一八七五记;四求,改曰二十五;五求,三一二五是;六求,两价三三七五;七求,四三七五置;八求,转身变作五。”(44) 用现代语言解释就是,1两=1/16斤=0.0625斤,2两=2/16斤=0.125斤, 3两=3/16斤=0.1875斤,4两=4/16斤=0.25斤,5两=5/16斤=0.3125斤, 6两=6/16斤=0.375斤,7两=7/16斤=0.4375斤,8两=8/16斤=0.5斤。 所以在具体的筹算实践中,杨辉总结了民间速算的方法和经验,并加以歌诀化,因而使算术捷法得到广泛传播。例如,乘数“二百一至三百”用杂法: 二百一,加三四加五;二百二,隔位加一倍之;二百三,七因两折加一六;二百四,加二加七;二百五,折半身前四因;二百六,倍之隔位加三;二百七,加三八加五;二百八,加三加六;二百九,加一加九;二一一,连身加一一;二一二,倍之隔位加六;二一三,加四二加五;二一四,倍之隔位加七;二一五,加七二三折半;二一六,加二加八;二一七,七因两折加二四;二一八,倍之隔位加九……二九八,二因加四九;二九九,加三退七七;三百,二因加五。(45) 所谓“二百一,加三四加五”是指当201作乘数时,先对被乘数作加34运算,接着再对所得结果作加5运算。当用202作乘数时,需先对被乘数作“隔位加一”(即被乘数进两位,另加上原被乘数与1的乘积)的运算,然后,再对所得结果加倍。其余类推,不作赘述。上述引文为杨辉“加因代乘三百题”中的后半部分,其算法多用“定身乘法”“一位乘法”“补数乘法”以及“折半”和兼用加、因、损、折几种算法,独不见“飞归法”。因此,清人李锐说:“《通变》卷内有代乘代除各三百题,今市井俗人所谓飞归法,正复相似。”(46)实际上,这是对杨辉算法的误解。对此,华印椿已有拨正。(47)当然,用现代珠算的观点看,杨辉上述方法未必简捷,但是在当时的历史条件下,《法算取用本末》所介绍的“代乘代除”法,对于筹算工具的改革和民间算法之捷化,起到了重要的推动作用,甚至有些算法,经过后人的进一步补充和完善,直到今天都有一定的应用价值。例如,中国台湾的王文佩通过长期的数学教学实践,发现对于中等程度的学生而言,“在学习过程中,对于基本观念的再次提醒、足够的示范及演练,确实有其存在的必要性。杨辉在乘除法的各‘三百题’,也为初学者和中等程度学习者,提供了更多的范例及学习机会。”(48) (责任编辑:admin) |
