|
三、《日用算法》中的“零两求分定数”问题 唐宋度量衡的量值愈来愈精确,这是唐宋变革的重要内容之一。例如,唐朝改隋朝以前的铢钱制为铢累钱制,规定每1钱等于2铢4累,而每10钱等于1两。入宋后,原来的铢累制已经无法适应宋代商品经济,尤其是微观计息和中药计量发展过程中所出现的新情况和新问题。于是,宋代废除了唐朝的铢累量值,而代之以两、钱、分、厘、毫、丝。据载,北宋刘承珪曾创制了比较精密和灵敏的1两戥秤(亦称“厘戥”,是一种单杠杆不等臂称器)和1钱半戥秤,(49)最小可称量1厘,合今0.04克,用于金银、药物等微量物品称重。然而,南宋的度量衡规模标准十分混乱,导致商贾及金融领域“分”与“两”的换算日趋多元化,故杨辉在《日用算法》中把“零两求分定数”作为一个独立问题进行专门阐释,目的在于尽可能将两分换算标准化。其“零两求分定数”云: 一两,六厘二毫半;二两,一分二厘半;三两,一分八厘七毫半;四两,二分半;五两,三分一厘二毫半;六两,三分七厘半;七两,四分三厘七毫半;八两,五分;九两,五分六厘二毫半;十两,六分二厘半;十一两,六分八厘七毫半;十二两,七分半;十三两,八分一厘二毫半;十四两,八分七厘半;十五两,九分三厘七毫半;十六两,十分;分还两,用加二五。(50) 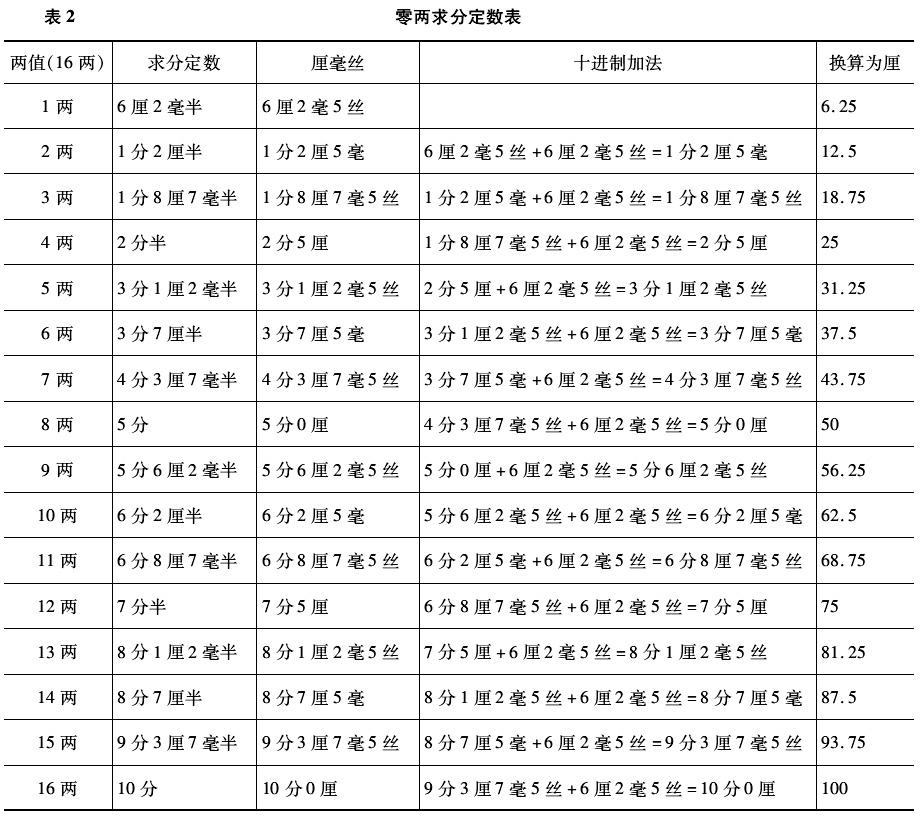 由表2可知,宋代衡不用铢作单位,而是用两、分、厘、毫、丝,1两等于10分,以下皆十进,10分等于100厘。 杨辉在《日用算法》序言中称,为解决初学者“无启蒙日用”的状况,“以乘除加减为法,秤斗尺田为问。编诗括十有三首,立图草六十六问……分上下卷首”。(51)可见,《日用算法》侧重于日常生活中所遇到的有关“秤、斗、尺、田”四个方面的数学问题,算法不外乘除加减,与《详解九章算法》和《杨辉算法》相比,《日用算法》的突出特点是“编诗括十有三首”。从思维学的角度讲,将算法诗歌化,便于记忆和传播,因而成为宋代普及乘除算法的一种重要方式。 如“立图草六十六问”(即66个问题)目前仅存一题三图草。其题云:“今有钱六贯八百文,买物一斤,问一两值几何?答曰:四百二十五文。”第一草曰:“斤价为实,置六贯八百文;四度折半,即是四次折半,得四百二十五;合问。”(52) 用现代数学式表示,则为 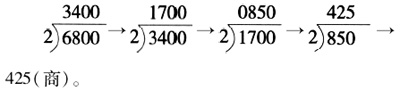 第二草曰:“斤价为实,置六贯八百文;如念法,于尾位求起,百上定十,先命八百为五十,后命六贯为三百七十五,共四百二十五;合问。”(53)第三草曰:“斤价为实折半,取十六两为八两价;八归,是取八两为一两价。”(54)第四草曰:“斤价为身,身为存十减六,斤价分为十六两,存留十两价,减去六两,于价贯上定百为一两之价。”(55)第五草曰:“斤价为实,以十六两为法,除之,是以斤价分为十六处,求一两之价。”(56) 华印椿将上述算草想象如图2。(57)  图2 华印椿想象的算草 草术中所言“念法”,即下面的八句口诀:“一求隔位六二五,二求退位一二五,三求一八七五记,四求改曰二十五,五求三一二五是,六求两价三七五,七求四三七五置,八求转身变作五。”(58)“八”以后“斤求两价念法”杨辉没有给出,后来朱世杰在《算法启蒙》一书中补充了“八”至“十五”念法,体现了“斤求两价”水平逐渐由1位向2位提升,同时,更加快了筹算向珠算全面转化的历史进程,所以,“斤求两价念法”对普及珠算尤其是推动元明时期商业的发展无疑起到了积极作用。如明代晋商兼珠算家王文素著《算学宝鉴》,书中所载“两化为斤口诀”,不仅发展了杨辉的“斤求两价念法”及元代朱世杰的“斤下留法”口诀(因为“两化为斤口诀”系专为十六两秤珠算而编制的),而且成了后世人们所奉行的斤两法口诀,(59)直到20世纪70年代之后人们普遍采用十两秤,杨辉“两化为斤口诀”才彻底完成了它的历史使命。 (责任编辑:admin) |
